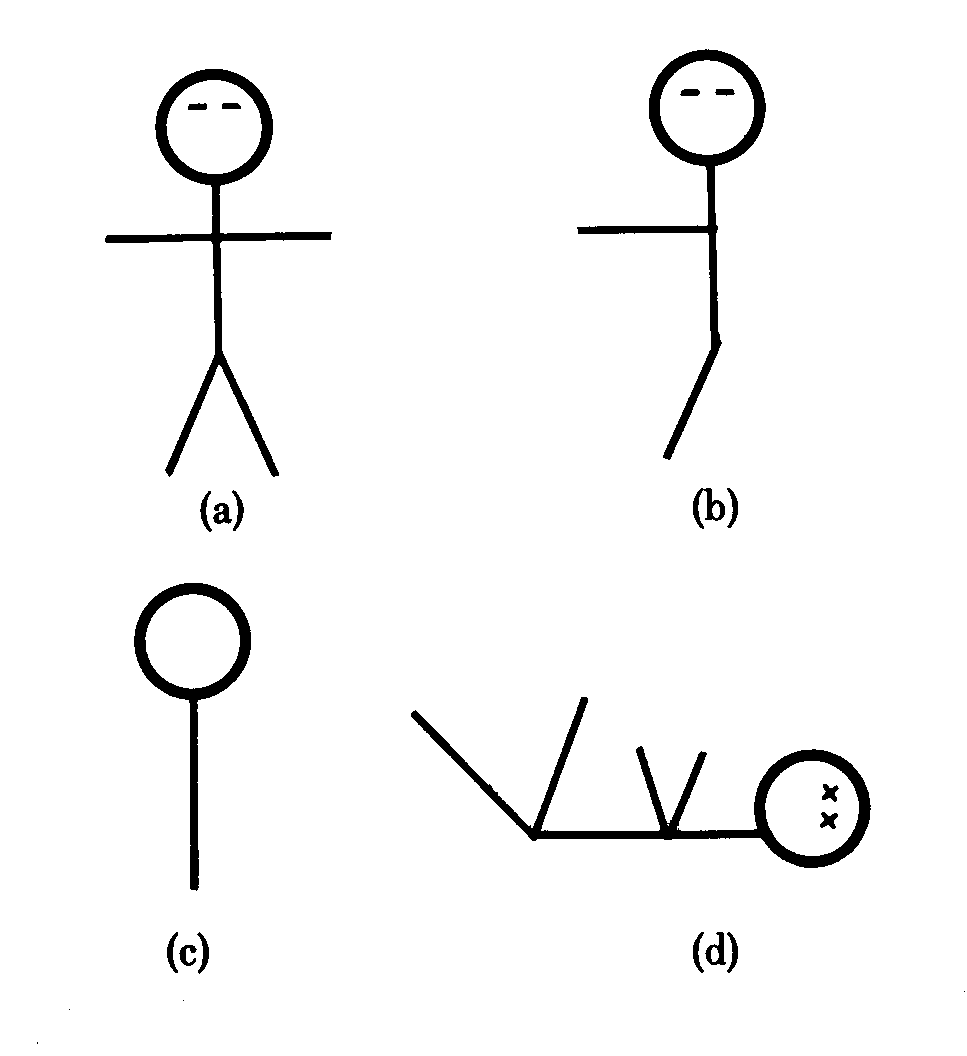Originally published in the
Journal of Irreproducible Results,
Vol. 27, No. 4, pp. 29-30, 1991.
Reprinted in
The Best of the Journal of Irreproducible Results,
George H. Scherr (ed.)
New York: Workman Publishing, 1983.
ISBN 0-89480-595-9.
Available in many technical bookstores in the humor section
and maybe at
amazon.com
or in
a library near you.
Abstract
An arm and a leg are not worth two eyes, they are worth less.
Introduction
Have you ever noticed how life insurance companies decide the relative worth of parts of our bodies? I just read a policy from Montgomery Ward (they will ,sell anything) that offered $6,000 "for loss of one hand, one foot, or the sight of one eye," and $12,000 "for death or loss of both hands, feet, the sight of both eyes, or any combination of these"
Ward seems to have assumed that hands, feet, and eyes are of equal worth, and that two of the same parts are worth exactly twice one. To me, a hand is worth a lot more than a foot, and the loss of two eyes is much worse than twice the loss of one; in the former
case, the injured party can not see. Not only that, in terms of payoffs, losing your eyes is as good as being dead, with which I do not agree.
The present study is directed at finding the psychological worth people attribute to various parts of our bodies. The principal hypotheses were that the pain of losing two similar parts is worse than twice the pain of losing one; that some parts of our bodies are valued more than others (notably that feet are least valued), that there will be a preference for people to retain their dominant hands (while no such preference will exist for eyes or feet); and finally that death is a lot worse than the loss of two similar parts, although it may be better than being a blind quadriplegic.
Method
|
The use of human subjects was deemed inappropriate by some of my colleagues, so rats were subjected to assorted treatments. Suffice it to say that the rats' ratings (especially those in the "death" condition) were ambiguous. An alternative method was devised.
Human subjects were asked to rate on a happy/sad scale how they would feel after the loss of factorially deleted parts of their bodies. To help them make these judgments, drawings corresponding to their supposed disabilities were presented along with vivid verbal descriptions. An example of an undisabled person is in Fig. 1a; while one missing an arm and a leg is depicted in Fig. 1b. A picture of the worst possible nonterminal deletion of parts is in Fig. 1c. Dead figures were represented as lying down, with x's in their eyes (regardless of whether they had lost any eyes), Fig. 1d.
While the use of subjects' ratings of how they would feel if they sustained these injuries might not lead to the same results as in the case when they actually incur the disabilities, I ignored this.
|
Figure 1: Examples of Stimuli
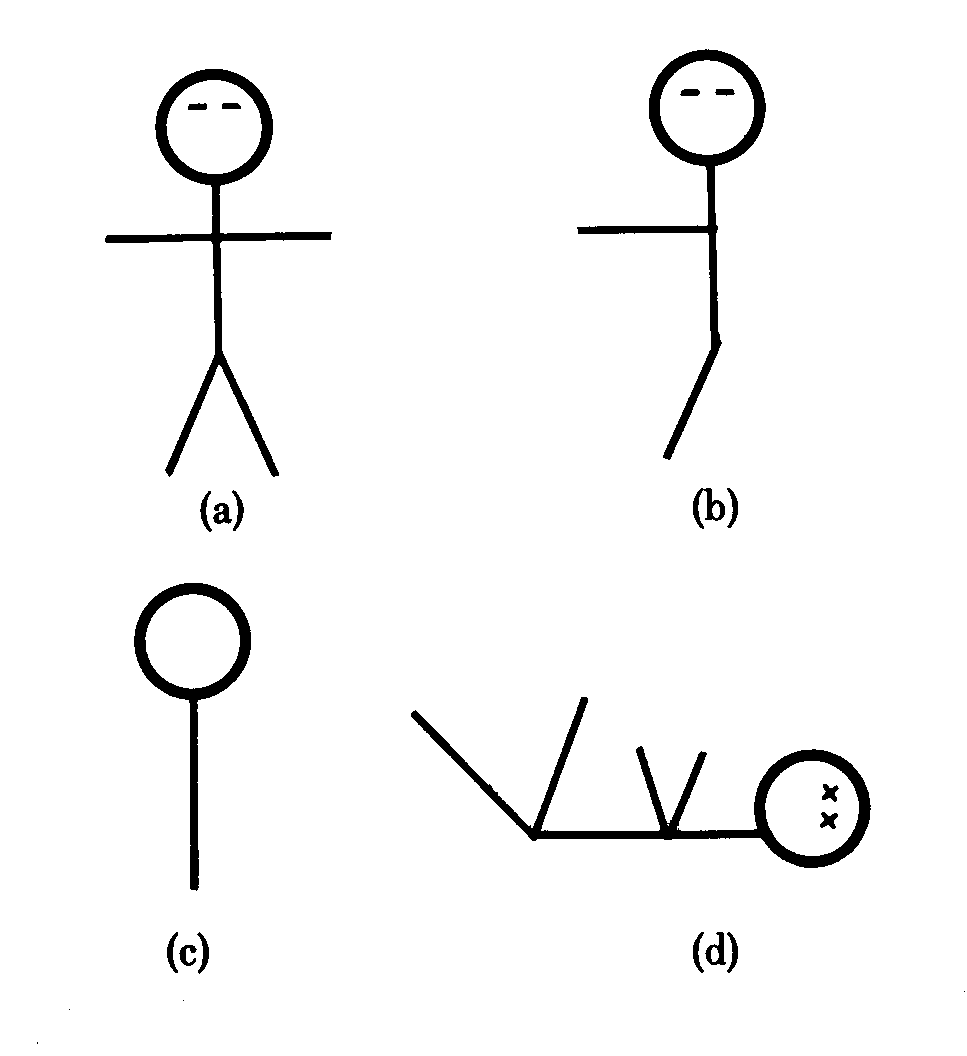
|
Results
|
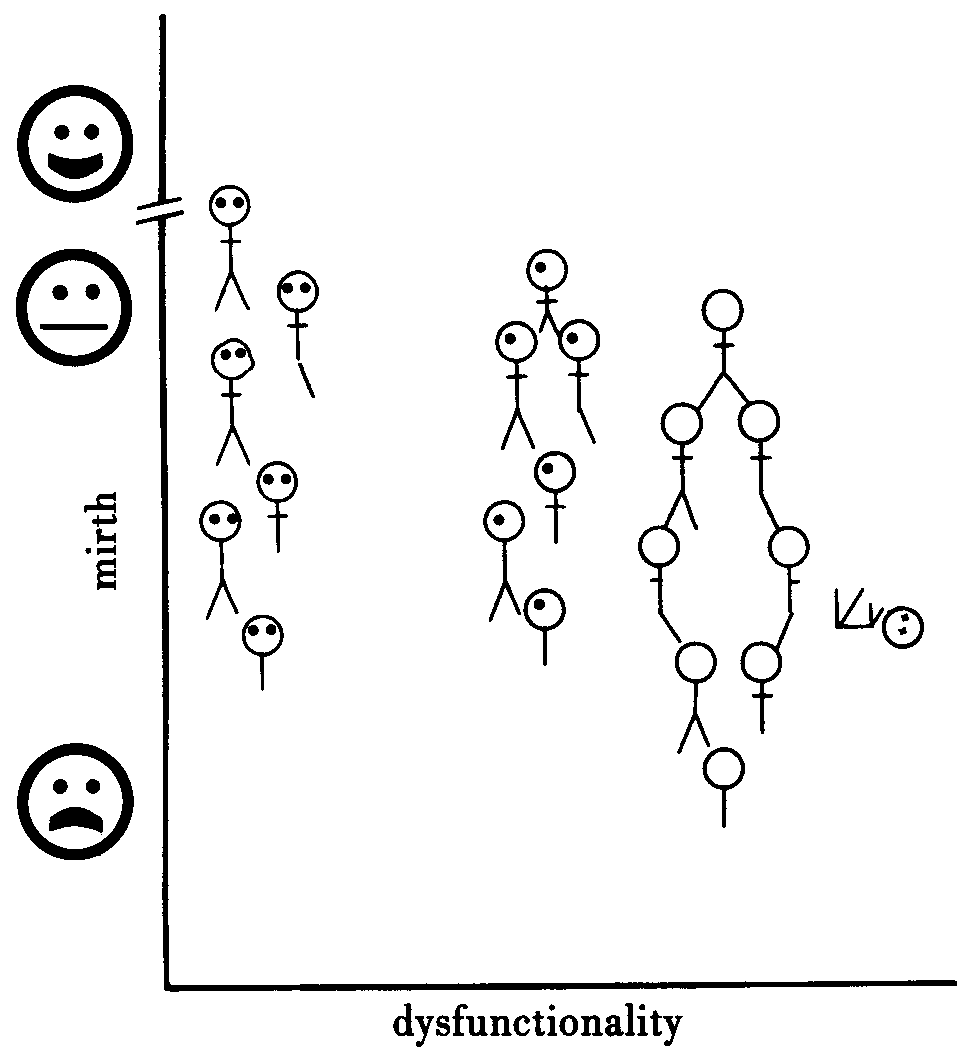
The data are presented in Fig. 2. Plotted are the average happiness ratings of subjects according to how many of each limb was lost. It is clear that subjects preferred to lose feet over hands, and preferred
to lose hands over eyes. Virtually all subjects showed more than twice the dismay at losing two similar limbs than losing one, which is consistent with my theory. Subjects reliably preferred their dominant hands (p = .05), but there was no dominance preference for eyes or feet (p = .06). As predicted by Law 4 of my theory, people preferred multiple losses over death; the
breaking point was when at least both hands and both eyes were lost. In these cases, people preferred death.
I should note that two subjects' data were discarded. Subject IA was found to be an insurance agent, who conformed exactly to the insurance companies' guidelines, making his data unacceptable. The other subject, SM, did not seem to understand the rating scale and gave happiness ratings positively correlated with the number of missing limbs. Additionally, SM rated that he preferred to be dead than have no missing parts, and his most preferred state was as depicted in Fig. 1c. Other subjects had no difficulties using the rating scale.
|
Figure 2: Mirth as a Function of Dysfunctionality
|
Discussion
The practical implications of this study and my theory are enormous. Insurance companies no longer need guess the amount of retribution to a permanently disabled party. Using the regression equation below they can figure the exact amount of misery of living victims and pay accordingly. Quadriplegics no longer need feel cheated because they were paid only once; they will get their fair share. In the equation, e is the number of eyes lost, h is the number of hands lost, and f is the number of feet lost.
payoff = $10,000 e + $8,000 h + $6,000 f
A correction factor can be applied to account for the greater subjective value of dominant hands. If a dominant hand is lost, then the corrected number of hands lost is 1.25, and if the non-dominant hand is lost, the corrected number of hands lost is 0.75.
I owe nothing to anyone concerning this research. I did it all myself. Maureen Graham of the St. Andrew's University did not inspire me at all, not a bit. Anyway, she has left the country.